// Juanpe Bolívar
// https://sinusoid.al

postmodern

immutable

data structures

Part I

The tragedy
of the
value based
architecture



mutability ⇒ ( pass by value ⇒ copying )

root cause cause problem 

const auto v0 = vector<int>{};
const auto v1 = v0.push_back(15);
const auto v2 = v1.push_back(16);
const auto v3 = v2.set(0, 42);


assert(v2.size() == v0.size() + 2);
assert(v3[0] - v1[0] == 27);
immutable data structure

one with all methods
marked const


persistent data structure

old values are preserved

structural sharing
  • no copying
  • compact history
  • fast comparison

immer
a library of immutable data structures

https://sinusoid.es/immer

  • idiomatic
    this is C++ not Haskell
  • performant
    cache-efficient, benchmark-driven
  • customizable
    stackable allocators, optional GC, thread-safety

Part II

in search of a magical vector 






const auto v0 = list<char>{{'a'}};
const auto v1 = v0.push_front('b')
                  .push_front('c');
const auto v2 = v1.push_front('d');
const auto v3 = v1.push_front('e');


Chris Okasaki
Purely Functional Data Structures

https://www.cs.cmu.edu/~rwh/theses/okasaki.pdf



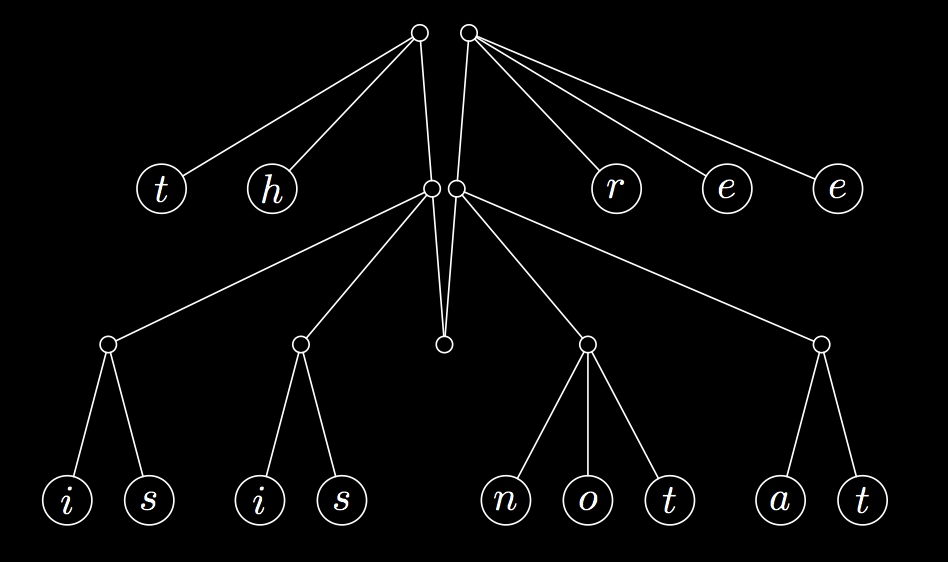
Ralf Hinze and Ross Paterson
Finger Trees: A General-purpose Data Structure

http://www.staff.city.ac.uk/~ross/papers/FingerTree.html

Phil Bagwell
Array Mapped Tries. 2000
RRB-Trees: Efficient Immutable Vectors. 2011

https://infoscience.epfl.ch/record/64394/files/triesearches.pdf
https://infoscience.epfl.ch/record/169879/files/RMTrees.pdf


Radix Balanced Tree

$M=2^B$ $M=32$ $B=5$ $\left\lceil\log_{32}(2^{32})\right\rceil = 7$

Radix Balanced Search

v[17] → 01 00 01 v.set(17, 'R')

Operations

$$\text{effective}\ O(1)$$
  • Random access
  • Update
  • Push back
  • Slice right
$$O(n)$$
  • Insert
  • Concat
  • Push front
  • Slice left

Relaxed Radix Balanced Tree

Operations

$$\text{effective}\ O(1)$$
  • Random access
  • Update
  • Push back
  • Slice right/right
$$O(\log(n))$$
  • Concat
  • Insert
  • Push front

Embedding
Radix balanced tree

$$M=2^B$$ $$M_l=2^{B_l}$$
$$ B_l^{\mathit{opt}}(B, T) = \left\lfloor \log_2\left( \frac{\mathit{sizeof}_* \times 2^B} {\mathit{sizeof}_T} \right) \right\rfloor $$ 

vector<int> myiota(vector<int> v, int first, int last)
{
    for (auto i = first; i < last; ++i)
        v = v.push_back(i);
    return v;
}

vector<int> myiota(vector<int> v, int first, int last)
{
    auto t = v.transient();
    for (auto i = first; i < last; ++i)
        t.push_back(i);
    return t.persistent();
}
          

vector<int> myiota(vector<int> v, int first, int last)
{
    auto t = v.transient();
    std::generate_n(std::back_inserter(t),
                    last - first,
                    [&] { return first++; });
    return t.persistent();
}

vector<int> myiota(vector<int> v, int first, int last)
{
    for (auto i = first; i < last; ++i)
        v = std::move(v).push_back(i);
    return v;
}

vector<char> say_hi(vector<char> v)
{
    return v.push_back('h')
            .push_back('i')
            .push_back('!');
}

Is this fast?

Summing a $10^5$ element vector ($\mu s$)
Ten $10^4$ element concatenations ($\mu s$)
Building a $10^5$ element vector ($\mu s$)
Building a $10^5$ element transient vector ($\mu s$)
Mutating all $10^5$ element vector ($\mu s$)
Mutating all $10^5$ element transient vector ($\mu s$)

YES.




Part III

I put a spell on my text editor

Demo time!


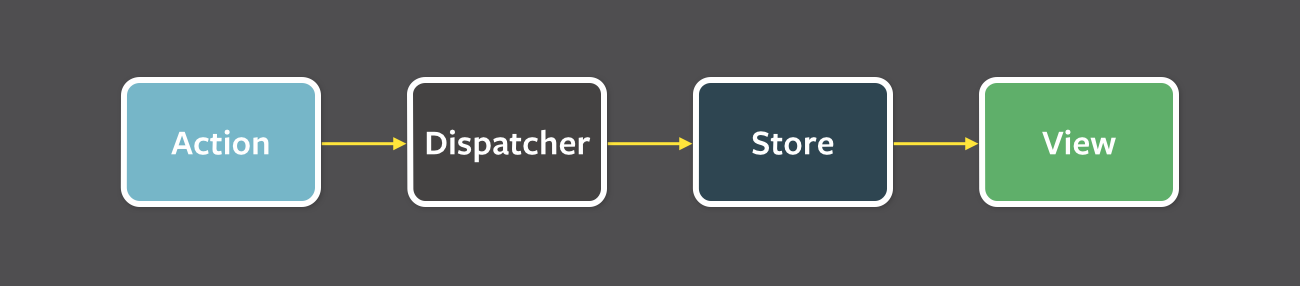
std::optional<application> update(application state, event ev);

int run(const char* fname)
{
    auto ui    = tui{};
    auto state = application{load_buffer(fname), key_map_emacs};
    draw(state);
    while (auto new_state = update(state, ui.next())) {
        state = *new_state;
        draw(state);
    }
    return 0;
}


using index = int;

struct coord
{
    index row = {};
    index col = {};
};

using line = immer::flex_vector<wchar_t>;
using text = immer::flex_vector<line>;

struct file
{
    immer::box<std::string> name;
    text content;
};

struct snapshot
{
    text content;
    coord cursor;
};
            

struct buffer
{
    file from;
    text content;
    coord cursor;
    coord scroll;
    boost::optional<coord> selection_start;
    immer::vector<snapshot> history;
    boost::optional<std::size_t> history_pos;
};

struct application
{
    buffer current;
    key_map keys;
    key_seq input;
    immer::vector<text> clipboard;
    immer::vector<message> messages;
};

struct event { key_code key; coord size; };

Afterword

programming and

https://github.com/arximboldi/immer
https://github.com/arximboldi/ewig
https://sinusoid.al
thanks. 

#1 edit                        S1 ♦
#2 edit                        S1   S2 ♦
#3 edit                        S1   S2   S3 ♦
#4 edit                        S1   S2   S3   S4 ♦
#5 undo                        S1   S2   S3 ♦ S4   S5
#6 undo                        S1   S2 ♦ S3   S4   S5   S6
#7 edit                        S1   S2   S3   S4   S5   S6  S7 ♦
          

buffer record(buffer before, buffer after)
{
    if (before.content != after.content) {
        after.history = after.history.push_back({before.content, before.cursor});
        if (before.history_pos == after.history_pos)
            after.history_pos = boost::none;
    }
    return after;
}

buffer undo(buffer buf)
{
    auto idx = buf.history_pos.value_or(buf.history.size());
    if (idx > 0) {
        auto restore = buf.history[--idx];
        buf.content = restore.content;
        buf.cursor = restore.cursor;
        buf.history_pos = idx;
    }
    return buf;
  }


buffer record(buffer before, buffer after)
{
    if (before.content != after.content) {
        after.history = after.history.push_back({before.content, before.cursor});
        if (before.history_pos == after.history_pos)
            after.history_pos = boost::none;
    }
    return after;
}

buffer undo(buffer buf)
{
    auto idx = buf.history_pos.value_or(buf.history.size());
    if (idx > 0) {
        auto restore = buf.history[--idx];
        buf.content = restore.content;
        buf.cursor = restore.cursor;
        buf.history_pos = idx;
    }
    return buf;
  }